Anna Vinnedge
United States Military Academy

Utilizing Machine Learning Models to Predict Success in Special Operations Assessment

The 75th Ranger Regiment is an elite Army Unit responsible for some of the most physically and mentally challenging missions. Entry to the unit is based on an assessment process called Ranger Regiment Assessment and Selection (RASP), which consists of a variety of tests and challenges of strength, intellect, and grit. This study explores the psychological and physical profiles of candidates who attempt to pass RASP. Using a Random Forest Artificial Intelligence model, and a penalized logistic regression model, we identify initial entry characteristics that are predictive of success in RASP. We focus on the differences between racial sub-groups and military occupational specialties (MOS) sub-groups to provide information for recruiters to identify underrepresented groups who are likely to succeed into the selection process.

Takayuki Iguchi
Florida State University

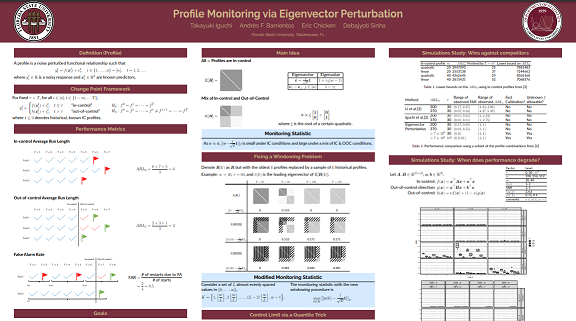
Profile Monitoring via Eigenvector Perturbation

Control charts are often used to monitor the quality characteristics of a process over time to ensure undesirable behavior is quickly detected. The escalating complexity of processes we wish to monitor spurs the need for more flexible control charts such as those used in profile monitoring. Additionally, designing a control chart that has an acceptable false alarm rate for a practitioner is a common challenge. Alarm fatigue can occur if the sampling rate is high (say, once a millisecond) and the control chart is calibrated to an average in-control run length (ARL0) of 200 or 370 which is often done in the literature. As alarm fatigue may not just be annoyance but result in detrimental effects to the quality of the product, control chart designers should seek to minimize the false alarm rate. Unfortunately, reducing the false alarm rate typically comes at the cost of detection delay or average out-of-control run length (ARL1). Motivated by recent work on eigenvector perturbation theory, we develop a computationally fast control chart called the Eigenvector Perturbation Control Chart for nonparametric profile monitoring. The control chart monitors the l_2 perturbation of the leading eigenvector of a correlation matrix and requires only a sample of known in-control profiles to determine control limits. Through a simulation study we demonstrate that it is able to outperform its competition by achieving an ARL1 close to or equal to 1 even when the control limits result in a large ARL0 on the order of 10^6. Additionally, non-zero false alarm rates with a change point after 10^4 in-control observations were only observed in scenarios that are either pathological or truly difficult for a correlation based monitoring scheme.

Brittany Fischer

Arizona State University

Optimal Designs for Multiple Response Distributions

Designed experiments can be a powerful tool for gaining fundamental understanding of systems and processes or maintaining or optimizing systems and processes. There are usually multiple performance and quality metrics that are of interest in an experiment, and these multiple responses may include data from nonnormal distributions, such as binary or count data. A design that is optimal for a normal response can be very different from a design that is optimal for a nonnormal response.
This work includes a two-phase method that helps experimenters identify a hybrid design for a multiple response problem. Mixture and optimal design methods are used with a weighted optimality criterion for a three-response problem that includes a normal, a binary, and a Poisson model, but could be generalized to an arbitrary number and combination of responses belonging to the exponential family. A mixture design is utilized to identify the optimal weights in the criterion presented.